并查集主要有两个功能:
- 将两个元素添加到一个集合中。
- 判断两个元素在不在同一个集合
将三个元素A,B,C (分别是数字)放在同一个集合,其实就是将三个元素连通在一起,如何连通呢。
只需要用一个一维数组来表示,即:father[A] = B,father[B] = C 这样就表述 A 与 B 与 C连通了(有向连通图)。
并查集模板:
1.初始化–init()
2.并查集里寻根–find(int u)
3.判断u和v是否同根–isSame(int u,int v)
4.将v->u加入并查集–join(int u,intv)
寻找存在的路径
题目描述
给定一个包含 n 个节点的无向图中,节点编号从 1 到 n (含 1 和 n )。
你的任务是判断是否有一条从节点 source 出发到节点 destination 的路径存在。
输入描述
第一行包含两个正整数 N 和 M,N 代表节点的个数,M 代表边的个数。
后续 M 行,每行两个正整数 s 和 t,代表从节点 s 与节点 t 之间有一条边。
最后一行包含两个正整数,代表起始节点 source 和目标节点 destination。
输出描述
输出一个整数,代表是否存在从节点 source 到节点 destination 的路径。如果存在,输出 1;否则,输出 0。
输入示例
5 4
1 2
1 3
2 4
3 4
1 4
2
3
4
5
6
输出示例
1
提示信息
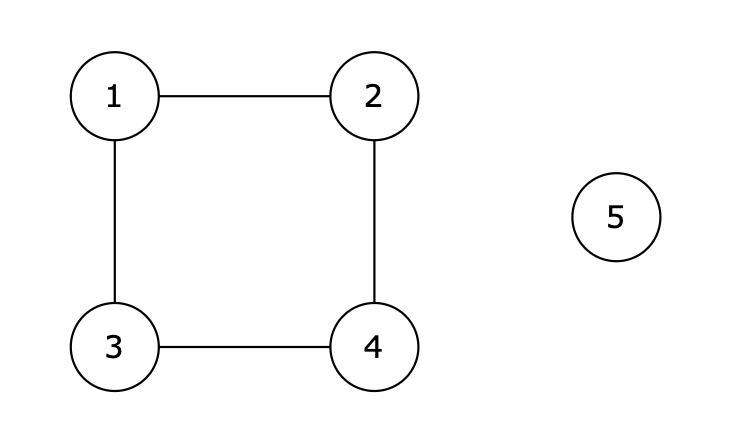
数据范围:
1 <= M, N <= 100。
思路:
将所有节点加入并查集,加入并查集相当于是构造出图了。
看给出的边对应的两个节点是否同根,同根即代表有路径。
ACM代码如下:
#include <iostream>
#include <vector>
using namespace std;
int N;
int n; // 边
vector<int> father;
void init() {
father = vector<int>(101, 0);
for (int i = 0; i < N; i++) {
father[i] = i;
}
}
int find(int u) {
if (father[u] == u) {
return u;
} else {
return father[u] = find(father[u]);
}
}
bool isSame(int u, int v) {
u = find(u);
v = find(v);
return u == v;
}
void join(int u, int v) {
u = find(u);
v = find(v);
if (u == v)
return;
father[v] = u;
}
int hasPath(const vector<vector<int>>& edge, int u, int v) {
init();
for (int i = 0; i < n; i++) {
join(edge[i][0], edge[i][1]);
}
return isSame(u, v);
}
int main() {
cin >> N >> n;
vector<vector<int>> edge(n, vector<int>(2, 0));
for (int i = 0; i < n; i++) {
cin >> edge[i][0] >> edge[i][1];
}
int source, destination;
cin >> source >> destination;
int res = hasPath(edge, source, destination);
cout << res << endl;
return 0;
}
树可以看成是一个连通且 无环 的 无向 图。
给定往一棵 n 个节点 (节点值 1~n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间,且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ,edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。
请找出一条可以删去的边,删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案,则返回数组 edges 中最后出现的那个。
示例 1:
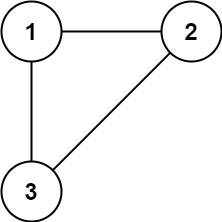
输入: edges = [[1,2], [1,3], [2,3]] 输出: [2,3]
示例 2:
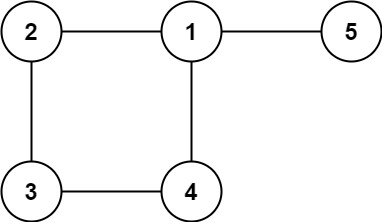
输入: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]] 输出: [1,4]
提示:
n == edges.length3 <= n <= 1000edges[i].length == 21 <= ai < bi <= edges.lengthai != biedges中无重复元素- 给定的图是连通的
思路:
题目说是无向图,返回一条可以删去的边,使得结果图是一个有着N个节点的树(即:只有一个根节点)。
如果有多个答案,则返回二维数组中最后出现的边。
那么我们就可以从前向后遍历每一条边(因为优先让前面的边连上),边的两个节点如果不在同一个集合,就加入集合(即:同一个根节点)。
如果边的两个节点已经出现在同一个集合里,说明着边的两个节点已经连在一起了,再加入这条边一定就出现环了。
代码如下:
class Solution {
private:
int n=1001;
vector<int> father=vector<int>(n,0);
void init(){
for(int i=0;i<n;i++){
father[i]=i;
}
}
int find(int i){
if(i==father[i]){
return i;
}
else{
return father[i]=find(father[i]);
}
}
bool isSame(int u,int v){
u=find(u);
v=find(v);
return u==v;
}
void join(int u,int v){
u=find(u);
v=find(v);
if(u==v) return;
father[v]=u;
}
public:
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
vector<int> res;
init();
for(int i=0;i<edges.size();i++){
if(isSame(edges[i][0],edges[i][1])){
res= edges[i];
}
else{
join(edges[i][0],edges[i][1]);
}
}
return res;
}
};
在本问题中,有根树指满足以下条件的 有向 图。该树只有一个根节点,所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点,而根节点没有父节点。
输入一个有向图,该图由一个有着 n 个节点(节点值不重复,从 1 到 n)的树及一条附加的有向边构成。附加的边包含在 1 到 n 中的两个不同顶点间,这条附加的边不属于树中已存在的边。
结果图是一个以边组成的二维数组 edges 。 每个元素是一对 [ui, vi],用以表示 有向 图中连接顶点 ui 和顶点 vi 的边,其中 ui 是 vi 的一个父节点。
返回一条能删除的边,使得剩下的图是有 n 个节点的有根树。若有多个答案,返回最后出现在给定二维数组的答案。
示例 1:
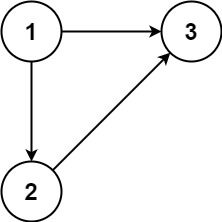
输入:edges = [[1,2],[1,3],[2,3]] 输出:[2,3]
示例 2:
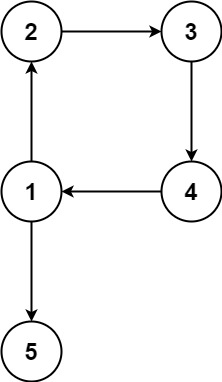
输入:edges = [[1,2],[2,3],[3,4],[4,1],[1,5]] 输出:[4,1]
提示:
n == edges.length3 <= n <= 1000edges[i].length == 21 <= ui, vi <= n
思路:
1. 并查集准备工作
-
定义一个固定大小的数组
father[]表示每个节点的父节点,用于并查集。 -
定义
n表示边的数量。 -
实现并查集的基础操作:
-
初始化:每个节点的父节点初始是自己。
-
查找根节点:带路径压缩的
find()。 -
合并两个集合:将两个节点所在集合合并。
-
判断两个节点是否属于同一集合。
-
2. 判断一组边删除后是否构成树
-
初始化并查集。
-
遍历所有边,跳过指定删除的那条边。
-
对于每一条边,判断是否会形成环:
-
如果两个端点已经在同一个集合中,说明成环,不是树。
-
否则将它们合并。
-
3. 找到成环的边(无入度为2的节点时)
-
初始化并查集。
-
遍历所有边:
-
如果当前边的两个端点已经连通(即
same()返回 true),说明这条边成环,应删除。 -
否则合并。
-
4. 主函数逻辑:寻找冗余边
-
初始化一个入度数组,用于记录每个节点的入度。
-
遍历所有边,统计入度。
-
找出所有入度为2的边(因为最多只有一个节点入度为2,对应最多两条边):
-
为保证题意(返回最后出现在数组中的边),倒序查找。
-
-
分情况讨论:
-
情况1或2:存在一个入度为2的节点
-
尝试删除这两条边中的一条,看哪一条删除后图变为树。
-
-
情况3:没有入度为2的节点
-
说明图中形成了有向环,找出形成环的边返回。
-
-
代码如下:
class Solution {
private:
int N = 1001;
vector<int> father = vector<int>(N, 0);
int n; // 边
void init() {
for (int i = 0; i < N; i++) {
father[i] = i;
}
}
int find(int u) {
if (father[u] == u) {
return u;
} else {
return father[u] = find(father[u]);
}
}
void join(int u, int v) {
u = find(u);
v = find(v);
if (u == v) {
return;
}
father[v] = u;
}
bool isSame(int u, int v) {
u = find(u);
v = find(v);
return u == v;
}
bool isRemoveEdgeToTree(const vector<vector<int>>& edges, int delEdge) {
init();
for (int i = 0; i < n; i++) {
if (i == delEdge)
continue;
if (isSame(edges[i][0], edges[i][1])) {
return false;
} else {
join(edges[i][0], edges[i][1]);
}
}
return true;
}
int findCycleEdge(const vector<vector<int>>& edges) {
init();
for (int i = 0; i < n; i++) {
if (isSame(edges[i][0], edges[i][1])) {
return i; // 找到导致环的边
}
join(edges[i][0], edges[i][1]);
}
return -1; // 没找到环
}
public:
vector<int> findRedundantDirectedConnection(vector<vector<int>>& edges) {
n = edges.size();
vector<int> inputVec(N, 0); // 入度数组
for (int i = 0; i < n; i++) {
inputVec[edges[i][1]]++;
}
vector<int> candidateEdges; // 存入度为2的节点对应的两条边的边编号
for (int i = n - 1; i >= 0; i--) {
if (inputVec[edges[i][1]] == 2) {
candidateEdges.push_back(i);
}
}
if (!candidateEdges.empty()) {
if (isRemoveEdgeToTree(edges, candidateEdges[0])) {
return edges[candidateEdges[0]];
} else {
return edges[candidateEdges[1]];
}
}
int cycleEdge = findCycleEdge(edges);
if (cycleEdge != -1) {
return edges[cycleEdge];
}
return {};
}
};




暂无评论