给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [ ["1","1","1","1","0"], ["1","1","0","1","0"], ["1","1","0","0","0"], ["0","0","0","0","0"] ] 输出:1
示例 2:
输入:grid = [ ["1","1","0","0","0"], ["1","1","0","0","0"], ["0","0","1","0","0"], ["0","0","0","1","1"] ] 输出:3
思路:
遇到一个没有遍历过的节点陆地,计数器就加一,然后把该节点陆地所能遍历到的陆地都标记上。
在遇到标记过的陆地节点和海洋节点的时候直接跳过。 这样计数器就是最终岛屿的数量。
那么可以DFS也可以BFS
深度优先搜素(DFS)版代码:
class Solution {
public:
int numIslands(vector<vector<char>>& grid) {
vector<vector<bool>> visited(grid.size(),
vector<bool>(grid[0].size(), false));
int res = 0;
for (int i = 0; i < grid.size(); i++) {
for (int j = 0; j < grid[0].size(); j++) {
if (!visited[i][j] && grid[i][j] == '1') {
res++;
dfs(grid, visited, i, j);
}
}
}
return res;
}
int dir[4][2] = {{0, 1}, // 右
{1, 0}, // 下
{-1, 0}, // 上
{0, -1}}; // 左
void dfs(const vector<vector<char>>& grid, vector<vector<bool>>& visited,
int x, int y) {
if (visited[x][y] || grid[x][y] == '0')
return;
visited[x][y] = true;
for (int i = 0; i < 4; i++) {
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 ||
nexty >= grid[0].size()) {
continue;
}
dfs(grid, visited, nextx, nexty);
}
}
};
广度优先搜索(BFS)版代码:
class Solution {
public:
int numIslands(vector<vector<char>>& grid) {
vector<vector<bool>> visited(grid.size(),
vector<bool>(grid[0].size(), false));
int res = 0;
for (int i = 0; i < grid.size(); i++) {
for (int j = 0; j < grid[0].size(); j++) {
if (!visited[i][j] && grid[i][j] == '1') {
res++;
bfs(grid, visited, i, j);
}
}
}
return res;
}
int dir[4][2] = {{0, 1}, // 右
{1, 0}, // 下
{-1, 0}, // 上
{0, -1}}; // 左
void bfs(const vector<vector<char>>& grid, vector<vector<bool>>& visited,
int x, int y) {
queue<pair<int, int>> que;
que.push({x, y});//起始节点加入队列
visited[x][y] = true; // 只要加入队列,立刻标记
while (!que.empty()) {
//从队列中取元素
pair<int, int> cur = que.front();
que.pop();
int curx = cur.first;
int cury = cur.second;
for (int i = 0; i < 4; i++) {
int nextx = curx + dir[i][0];
int nexty = cury + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 ||
nexty >= grid[0].size())
continue; // 越界了,直接跳过
if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') {
que.push({nextx, nexty});
visited[nextx][nexty] = true; // 只要加入队列立刻标记
}
}
}
}
};
给你一个大小为 m x n 的二进制矩阵 grid 。
岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
岛屿的面积是岛上值为 1 的单元格的数目。
计算并返回 grid 中最大的岛屿面积。如果没有岛屿,则返回面积为 0 。
示例 1:
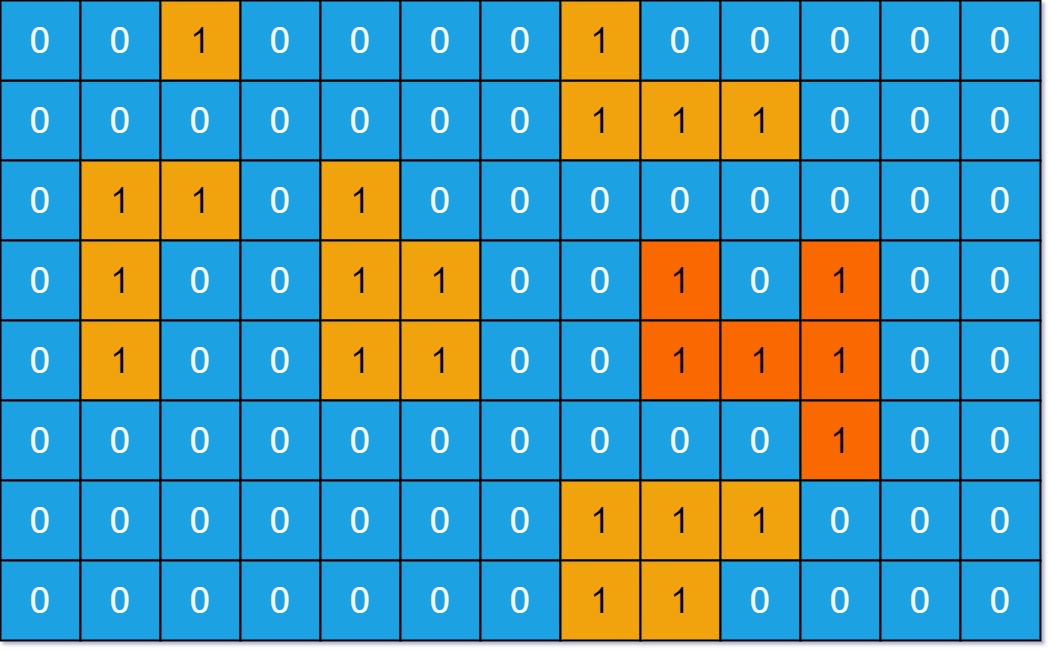
输入:grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]] 输出:6 解释:答案不应该是11,因为岛屿只能包含水平或垂直这四个方向上的1。
示例 2:
输入:grid = [[0,0,0,0,0,0,0,0]] 输出:0
思路:
这道题目也是 dfs bfs基础类题目,就是搜索每个岛屿上“1”的数量,然后取一个最大的。
本题思路上比较简单,难点其实都是 dfs 和 bfs的理论基础。
dfs处理当前节点的相邻节点,即在主函数遇到岛屿就计数为1,dfs处理接下来的相邻陆地
代码如下:
class Solution {
public:
int maxAreaOfIsland(vector<vector<int>>& grid) {
int res = 0;
vector<vector<bool>> visited(grid.size(),
vector<bool>(grid[0].size(), 0));
for (int i = 0; i < grid.size(); i++) {
for (int j = 0; j < grid[0].size(); j++) {
if (!visited[i][j] && grid[i][j] == 1) {
count = 1;
visited[i][j] = true;
dfs(grid, visited, i, j);
res = max(res, count);
}
}
}
return res;
}
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1};
int count = 0;
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x,
int y) {
for (int i = 0; i < 4; i++) {
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 ||
nexty >= grid[0].size()) {
continue;
}
if (!visited[nextx][nexty] && grid[nextx][nexty] == 1) {
visited[nextx][nexty] = true;
count++;
dfs(grid, visited, nextx, nexty);
}
}
}
};
bfs版:
class Solution {
public:
int maxAreaOfIsland(vector<vector<int>>& grid) {
int res = 0;
vector<vector<bool>> visited(grid.size(),
vector<bool>(grid[0].size(), 0));
for (int i = 0; i < grid.size(); i++) {
for (int j = 0; j < grid[0].size(); j++) {
if (!visited[i][j] && grid[i][j] == 1) {
count = 1;
visited[i][j] = true;
bfs(grid, visited, i, j);
res = max(res, count);
}
}
}
return res;
}
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1};
int count = 0;
void bfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x,
int y) {
queue<pair<int, int>> que;
que.push({x, y}); // 起始节点
visited[x][y] = true;
while (!que.empty()) {
pair<int, int> cur = que.front();
que.pop();
int curx = cur.first;
int cury = cur.second;
for (int i = 0; i < 4; i++) {
int nextx = curx + dir[i][0];
int nexty = cury + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 ||
nexty >= grid[0].size()) {
continue;
}
if (!visited[nextx][nexty] && grid[nextx][nexty] == 1) {
visited[nextx][nexty] = 1;
count++;
que.push({nextx, nexty});
}
}
}
}
};
给定一个 row x col 的二维网格地图 grid ,其中:grid[i][j] = 1 表示陆地, grid[i][j] = 0 表示水域。
网格中的格子 水平和垂直 方向相连(对角线方向不相连)。整个网格被水完全包围,但其中恰好有一个岛屿(或者说,一个或多个表示陆地的格子相连组成的岛屿)。
岛屿中没有“湖”(“湖” 指水域在岛屿内部且不和岛屿周围的水相连)。格子是边长为 1 的正方形。网格为长方形,且宽度和高度均不超过 100 。计算这个岛屿的周长。
示例 1:
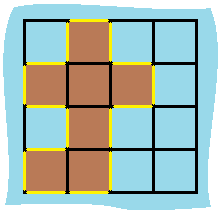
输入:grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]] 输出:16 解释:它的周长是上面图片中的 16 个黄色的边
示例 2:
输入:grid = [[1]] 输出:4
示例 3:
输入:grid = [[1,0]] 输出:4
思路:
岛屿问题最容易让人想到BFS或者DFS,避免大家惯性思维,这题是不用的。
那遍历图去推就好。
当检测到陆地时,只需检查右和下是否有陆地,如有则减2就好。
代码如下:
class Solution {
public:
int islandPerimeter(vector<vector<int>>& grid) {
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1};
int res = 0;
for (int i = 0; i < grid.size(); i++) {
for (int j = 0; j < grid[0].size(); j++) {
if (grid[i][j] == 1) {
res += 4;
for (int k = 0; k < 2; k++) {
int nextx = i + dir[k][0];
int nexty = j + dir[k][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 ||
nexty >= grid[0].size()) {
continue;
}
if (grid[nextx][nexty] == 1) {
res -= 2;
}
}
}
}
}
return res;
}
};




暂无评论