图
整体上一般分为 有向图 和 无向图。
有向图是指 图中边是有方向的。
无向图是指 图中边没有方向。
加权有向(无向)图,就是图中边是有权值的。
度
无向图中有几条边连接该节点,该节点就有几度。
在有向图中,每个节点有出度和入度。
出度:从该节点出发的边的个数。
入度:指向该节点边的个数。
连通性
在无向图中,任何两个节点都是可以到达的,称之为连通图。
如果有节点不能到达其他节点,则为非连通图。
在有向图中,任何两个节点是可以相互到达的,称之为 强连通图。
在无向图中的极大连通子图称之为该图的一个连通分量。
在有向图中极大强连通子图称之为该图的强连通分量。
图的遍历方式
图的遍历方式基本是两大类:
- 深度优先搜索(dfs)
- 广度优先搜索(bfs)
区别:
- dfs是可一个方向去搜,不到黄河不回头,直到遇到绝境了,搜不下去了,再换方向(换方向的过程就涉及到了回溯)。
- bfs是先把本节点所连接的所有节点遍历一遍,走到下一个节点的时候,再把连接节点的所有节点遍历一遍,搜索方向更像是广度,四面八方的搜索过程。
图的构造
给你一个有 n 个节点的 有向无环图(DAG),请你找出所有从节点 0 到节点 n-1 的路径并输出(不要求按特定顺序)
graph[i] 是一个从节点 i 可以访问的所有节点的列表(即从节点 i 到节点 graph[i][j]存在一条有向边)。
示例 1:

输入:graph = [[1,2],[3],[3],[]] 输出:[[0,1,3],[0,2,3]] 解释:有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3
示例 2:

输入:graph = [[4,3,1],[3,2,4],[3],[4],[]] 输出:[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]
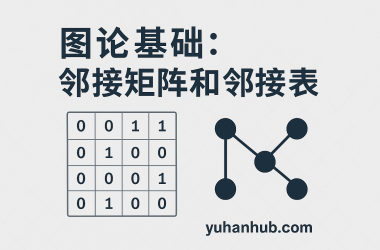
邻接矩阵表示法:
邻接矩阵 使用 二维数组来表示图结构。 邻接矩阵是从节点的角度来表示图,有多少节点就申请多大的二维数组。
ACM代码如下:
#include <iostream>
#include <vector>
using namespace std;
vector<vector<int>> res;
vector<int> path;
void dfs(const vector<vector<int>>& graph,int x,int n){
if(x==n){
res.push_back(path);
return;
}
for(int i=1;i<=n;i++){
if(graph[x][i]==1){//找到与x连接的节点
path.push_back(i);
dfs(graph,i,n);
path.pop_back();
}
}
}
int main(){
int n,m,s,t;
cin>>n>>m;
vector<vector<int>> graph(n+1,vector<int>(n+1,0));
while(m--){
cin>>s>>t;
graph[s][t]=1;//邻接矩阵表示,1表示相连
}
path.push_back(1);
dfs(graph,1,n);
if(res.size()==0) cout<<-1<<endl;
for(const vector<int> &pa:res){
for(int i=0;i<pa.size()-1;i++){
cout<<pa[i]<<" ";
}
cout<<pa[pa.size()-1]<<endl;
}
}
邻接表表示法:
邻接表 使用 数组 + 链表的方式来表示。 邻接表是从边的数量来表示图,有多少边 才会申请对应大小的链表。
ACM代码如下:
#include<iostream>
#include<vector>
#include<list>
using namespace std;
vector<vector<int>> res;
vector<int> path;
void dfs(const vector<list<int>>& graph,int x,int n){
if(x==n){
res.push_back(path);
return;
}
for(int i:graph[x]){
path.push_back(i);
dfs(graph,i,n);
path.pop_back();
}
}
int main(){
int n,m,s,t;
cin>>n>>m;
vector<list<int>> graph(n+1);
while (m--){
cin>>s>>t;
graph[s].push_back(t);//邻接表,表示s->t
}
path.push_back(1);
dfs(graph,1,n);
if(res.size()==0) cout<<-1<<endl;
for(const vector<int> &pa:res){
for(int i=0;i<pa.size();i++){
cout<<pa[i]<<" ";
}
cout<<pa[pa.size()-1]<<endl;
}
}



暂无评论