给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6 解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1] 输出:1
示例 3:
输入:nums = [5,4,-1,7,8] 输出:23
思路:
很容易想到暴力方法,但是超时了。
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int res = INT_MIN;
for (int i = 0; i < nums.size(); i++) {
int sum = 0;
for (int j = i; j < nums.size(); j++) {
sum += nums[j];
res = max(res, sum);
}
}
return res;
}
};
那这道题该怎么贪呢?贪就贪在sum不能是负数!
当遇到负数就应该灵醒一点,因为之前到现在sum是负数还不如断了重新算呢。这样就不用两个循环了。
代码如下:
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int res = INT_MIN;
int sum = 0;
for (int i = 0; i < nums.size(); i++) {
sum += nums[i];
res = max(res, sum);
if (sum <= 0) {
sum = 0;//贪
}
}
return res;
}
};
在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
给定两个整数数组 gas 和 cost ,如果你可以按顺序绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1 。如果存在解,则 保证 它是 唯一 的。
示例 1:
输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2] 输出: 3 解释: 从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油 开往 4 号加油站,此时油箱有 4 - 1 + 5 = 8 升汽油 开往 0 号加油站,此时油箱有 8 - 2 + 1 = 7 升汽油 开往 1 号加油站,此时油箱有 7 - 3 + 2 = 6 升汽油 开往 2 号加油站,此时油箱有 6 - 4 + 3 = 5 升汽油 开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。 因此,3 可为起始索引。
示例 2:
输入: gas = [2,3,4], cost = [3,4,3] 输出: -1 解释: 你不能从 0 号或 1 号加油站出发,因为没有足够的汽油可以让你行驶到下一个加油站。 我们从 2 号加油站出发,可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油 开往 0 号加油站,此时油箱有 4 - 3 + 2 = 3 升汽油 开往 1 号加油站,此时油箱有 3 - 3 + 3 = 3 升汽油 你无法返回 2 号加油站,因为返程需要消耗 4 升汽油,但是你的油箱只有 3 升汽油。 因此,无论怎样,你都不可能绕环路行驶一周。
思路:
这题判断能不能走完全程很简单,只需要看总剩余油量是否大于0即可。不用担心中间断油,因为总有一个起始点可以满足走完全程。
暴力的思路,模拟以每个点做节点,看油在那个节点出发走完一圈不会断就可以。
但是超时无法AC,代码如下:
class Solution {
public:
int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
for (int i = 0; i < cost.size(); i++) {
int rest = gas[i] - cost[i]; // 记录剩余油量
int index = (i + 1) % cost.size();//用于保证在绕圈圈,很实用的小技巧
while (rest > 0 && index != i) { // 模拟以i为起点行驶一圈(如果有rest==0,那么答案就不唯一了)
rest += gas[index] - cost[index];
index = (index + 1) % cost.size();
}
// 如果以i为起点跑一圈,剩余油量>=0,返回该起始位置
if (rest >= 0 && index == i) return i;
}
return -1;
}
};
会超时,所以还是要用贪心算法。
局部最优:当前累加rest[i]的和curSum一旦小于0,起始位置至少要是i+1,因为从i之前开始一定不行。全局最优:找到可以跑一圈的起始位置。
可以看出来思路有点类似于上题53. 最大子数组和,都是当总量为负时断掉重算。
代码如下:
class Solution {
public:
int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
int totalgas = 0;
int curRestGas = 0;
int start = 0;
for (int i = 0; i < gas.size(); i++) {
totalgas += gas[i] - cost[i];
curRestGas += gas[i] - cost[i];
//开始贪!
if (curRestGas < 0) {
curRestGas = 0;
start = i + 1;
}
}
if (totalgas < 0) {
return -1;
}
return start;
}
};
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:
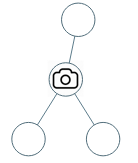
输入:[0,0,null,0,0] 输出:1 解释:如图所示,一台摄像头足以监控所有节点。
示例 2:
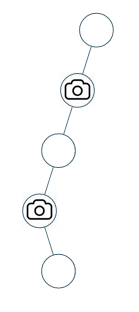
输入:[0,0,null,0,null,0,null,null,0] 输出:2 解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
思路:
局部最优: 每次递归时,当我们遇到某个节点时,我们选择尽量在节点上放置摄像头(如果该节点和它的子树没有被覆盖的话)。对于每个节点,我们总是选择能覆盖其子树的最优方案。
全局最优:摄像头最少且能覆盖整个二叉树。
明显要不要安摄像头是由其子树的摄像头监视情况决定的,所以从下到上遍历二叉树。
我们可以通过给节点赋值,通过值来判断其监视情况。
代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int minCameraCover(TreeNode* root) {
int res = 0;
if (dfs(root, res) == 0) {
res++; // 如果根节点没有被监控,添加一个摄像头
}
return res;
}
// 返回值含义:
// 0 -> 当前节点没有被覆盖
// 1 -> 当前节点有摄像头
// 2 -> 当前节点被覆盖
int dfs(TreeNode* node, int& res) {
if (node == nullptr) return 2; // 空节点不需要摄像头,视为已覆盖
int left = dfs(node->left, res); // 左子树状态
int right = dfs(node->right, res); // 右子树状态
if (left == 0 || right == 0) {
// 如果左或右子树没有被覆盖,那么当前节点需要一个摄像头
res++;
return 1; // 当前节点安装了摄像头
}
if (left == 1 || right == 1) {
// 如果左或右子树有摄像头,则当前节点被监控
return 2;
}
return 0; // 如果左、右子树都被覆盖,当前节点没有摄像头
}
};


暂无评论