给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵
二叉搜索树。
示例 1:

输入:nums = [-10,-3,0,5,9] 输出:[0,-3,9,-10,null,5] 解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:
示例 2:

输入:nums = [1,3] 输出:[3,1] 解释:[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。
之前在二叉搜索树的有序性中提到过二叉搜索树的中序遍历就是一个有序数组。
那么就取数组的中间值,按照中序遍历构造二叉树即可。
有个小细节,在取中间值时,不能(left+right)/2。
因为如果left和right同时是INT_MAX就不妙了。
所以mid=left+(right-left)/2才是对的。
代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
* right(right) {}
* };
*/
class Solution {
private:
TreeNode* traversal(vector<int>& nums, int left, int right) {
if (left > right)
return nullptr;
int mid = left + (right - left) / 2;
TreeNode* root = new TreeNode(nums[mid]);
root->left = traversal(nums, left, mid - 1);
root->right = traversal(nums, mid + 1, right);
return root;
}
public:
TreeNode* sortedArrayToBST(vector<int>& nums) {
TreeNode* root = traversal(nums, 0, nums.size() - 1);
return root;
}
};
另一道题也是一样的,只是没有把有序数组拍脸上而已。
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
示例 1:
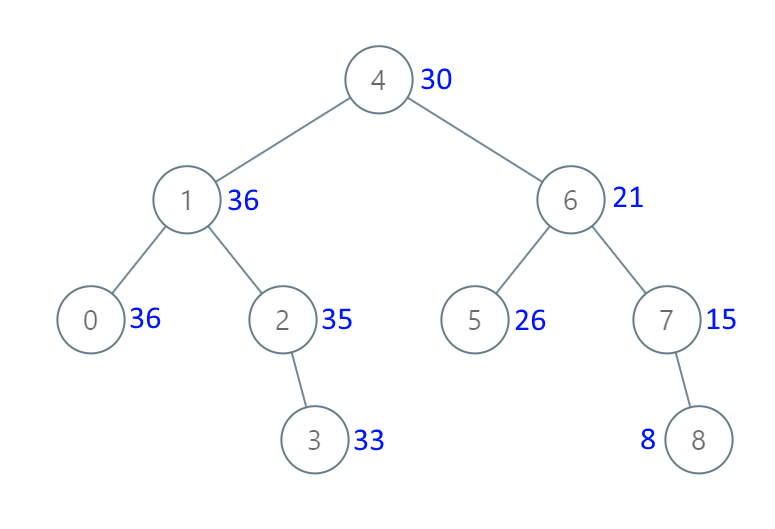
输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8] 输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2:
输入:root = [0,null,1] 输出:[1,null,1]
示例 3:
输入:root = [1,0,2] 输出:[3,3,2]
示例 4:
输入:root = [3,2,4,1] 输出:[7,9,4,10]
看图就很明显了,以前是右下角最大,现在变成右下角最小了,而且依然是有序数组,只是变成递减罢了。
那有序数组正着数是中序遍历,现在倒过来就是反中序遍历呗。
中序遍历左中右,现在就是右中左。
代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
* right(right) {}
* };
*/
class Solution {
int pre = 0;
void traversal(TreeNode* cur) {
if (cur == nullptr)
return;
traversal(cur->right); // 没有返回值就这样写。
cur->val += pre;
pre = cur->val;
traversal(cur->left);
return;
}
public:
TreeNode* convertBST(TreeNode* root) {
traversal(root);
return root;
}
};


暂无评论